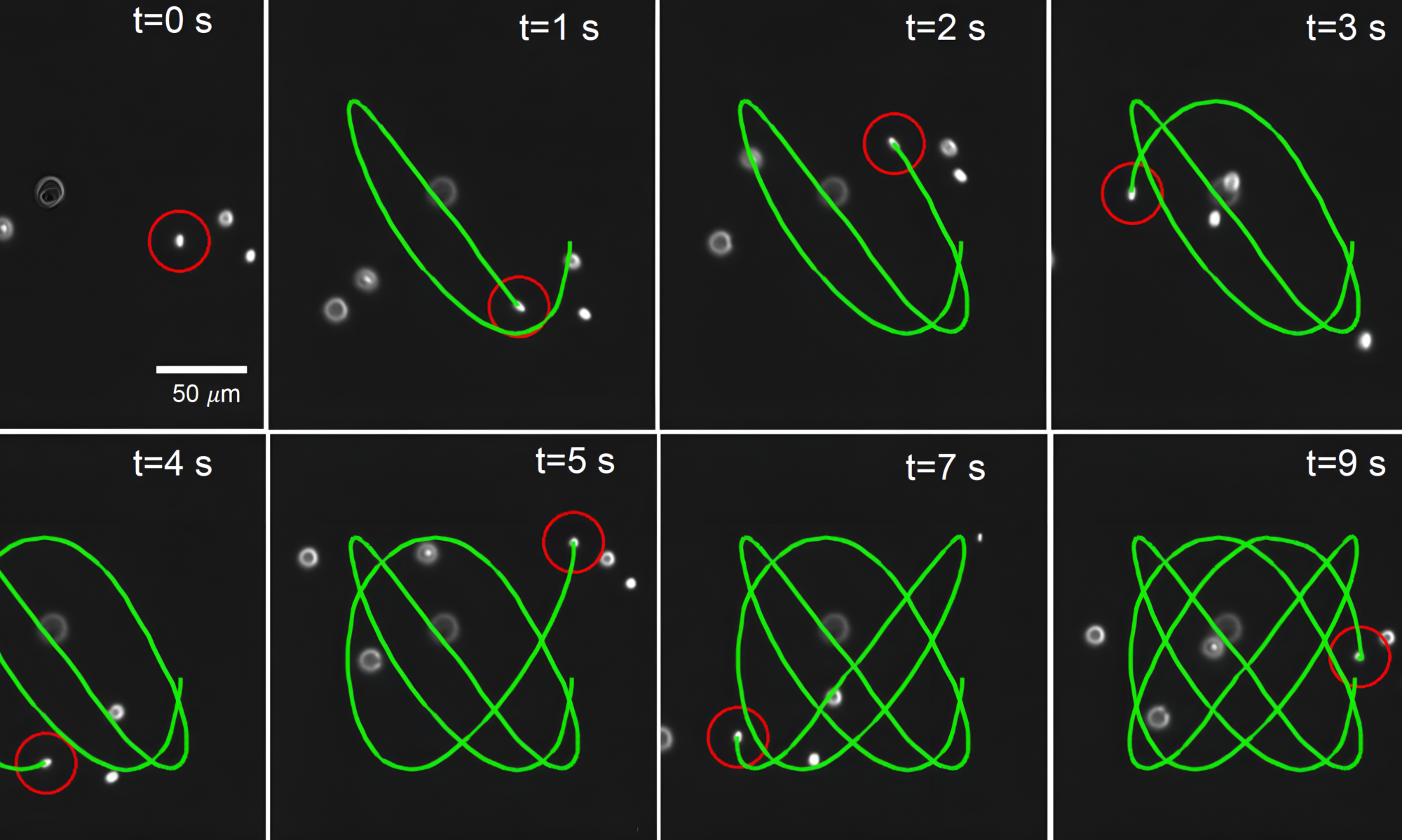
Understanding the dynamics of membrane-bound capsules and vesicles is critical for developing effective delivery reagents and for long-term stability of personal care products. Our group directly studies the conformational dynamics of lipid vesicles using fluorescence microscopy and automated flow control. We identified new modes of vesicle shape relaxation for highly deformed vesicles and fundamentally new stretching dynamics in the nonlinear regime. Our work continues to explore vesicle mechanical properties by directly observing vesicle conformations and shape dynamics in flow such as vesicle wrinkling and buckling using automated flow control.
Nonlinear transient and steady state stretching of vesicles in flow
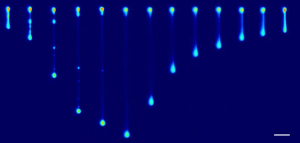Membrane-bound vesicles and organelles exhibit a wide array of nonspherical shapes at equilibrium, including biconcave and tubular morphologies. Despite recent progress, the stretching dynamics of deflated vesicles is not fully understood, particularly far from equilibrium where complex nonspherical shapes undergo large deformations in flow. Here, we directly observe the transient and steady-state nonlinear stretching dynamics of deflated vesicles in extensional flow using a Stokes trap. Automated flow control is used to observe vesicle dynamics over a wide range of flow rates, shape anisotropy, and viscosity contrast. Our results show that deflated vesicle membranes stretch into highly deformed shapes in flow above a critical capillary number Ca,c1. We further identify a second critical capillary number Ca,c2, above which vesicle stretch diverges in flow. Vesicles are robust to multiple nonlinear stretch−relax cycles, evidenced by relaxation of dumbbell-shaped vesicles containing thin lipid tethers following flow cessation. An analytical model is developed for vesicle deformation in flow, which enables comparison of nonlinear steady-state stretching results with theories for different reduced volumes. Our results show that the model captures the steady-state stretching of moderately deflated vesicles; however, it underpredicts the steady-state nonlinear stretching of highly deflated vesicles. Overall, these results provide a new understanding of the nonlinear stretching dynamics and membrane mechanics of deflated vesicles in flow.
Publication:
D. Kumar and C. M. Schroeder, “Nonlinear Transient and Steady-state Stretching of Deflated Vesicles in Flow”, Langmuir, 37, 13976-13984 (2021).
Flow-phase behavior of vesicles in extensional flow
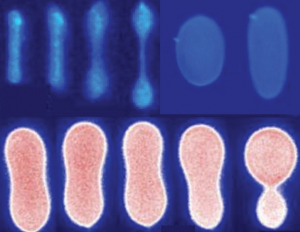Lipid vesicles play a key role in fundamental biological processes. Despite recent progress, we lack a complete understanding of the non-equilibrium dynamics of vesicles due to challenges associated with long-time observation of shape fluctuations in strong flows. In this work, we present a flow-phase diagram for vesicle shape and conformational transitions in planar extensional flow using a Stokes trap, which enables control over the center-of-mass position of single or multiple vesicles in precisely defined flows. In this way, we directly observe the non-equilibrium conformations of lipid vesicles as a function of reduced volume, capillary number, and viscosity contrast. Our results show that vesicle dynamics in extensional flow are characterized by the emergence of three distinct shape transitions, including a tubular to symmetric dumbbell transition, a spheroid to asymmetric dumbbell transition, and quasi-spherical to ellipsoid transition. The experimental phase diagram is in good agreement with recent predictions from simulations. We further show that the phase boundary of vesicle shape transitions is independent of the viscosity contrast. Taken together, our results demonstrate the utility of the Stokes trap for the precise quantification of vesicle stretching dynamics in precisely defined flows.
Publications:
Dinesh Kumar, Channing M. Richter, and Charles Schroeder, “Conformational dynamics and phase behavior of lipid vesicles in a precisely controlled extensional flow”, Soft Matter, 16, 337-347 (2020).
Other relevant publications:
- Dinesh Kumar, Channing M. Richter, and Charles Schroeder, “Double-mode relaxation of highly deformed vesicles”, Physical Review E, 102, 010605R (2020).